The many descendants of Tarski’s
Relation Algebras
Peter Jipsen
Vanderbilt
University
Alfred Tarski Centenary Conference, Warsaw, May 29,
2001
A story about the creation of Relation Algebras
In the beginning
there were algebras of concrete relations.
Tarski saw they were good, and he separated the interesting
ideas from the trivial ones.
And Tarski said “Let there be an abstract theory about these
algebras”.
So he made the theory of Relation Algebras. And he saw it
was good.
And then Tarski said “Let the theory produce all the known
results about concrete relations”. And it was so.
And he proved many interesting new results about relation
algebras, including a correspondence with 3-variable logic that allowed the
interpretation of set theory and he provided the first example of an
undecidable equational theory.
And Tarski said “Let the minds teem with new conjectures,
let ideas fly, and let the community produce many new related theories and
results”.
Thus the field of relation algebras was born, with its many applications and connections to other areas.
(all quotes fictitious; passage based on well known source)
And he did not rest. The trinity of Henkin, Monk, Tarski wrote two volumes about Cylindric Algebras (including several chapters on general algebra and relation algebras).
His many disciples worked tirelessly to spread the word.
And there was a cultural upheaval that made Tarski’s name
spread far and wide: computer science emerged as a major discipline.
Some statistics about Tarski:
Number of authored papers in MR:
Tarski 125
Erdös 1535 (the most
publications by any author)
Number of reviews mentioning name in MR:
Tarski 2133
Erdös 6878
Number of web pages mentioning name (on Google):
Tarski 36000
Erdös 30000
Number of papers in 11 major Mathematics journals that
mention Tarski: 1041
Number of papers in 10 major Philosophy journals that
mention Tarski: 1047
List of the journals searched in JSTOR:
Mathematics
(11 journals)
1.
American
Journal of Mathematics (1878-1995)
2.
American
Mathematical Monthly (1894-1995)
3.
Annals
of Mathematics (1884-1995)
4.
Journal
of Symbolic Logic (1936-1996)
5.
Journal
of the American Mathematical Society (1988-1995)
6.
Mathematics
of Computation (1960-1995)
7.
Proceedings
of the American Mathematical Society (1950-1995)
8.
SIAM
Journal on Applied Mathematics (1966-1995)
9.
SIAM
Journal on Numerical Analysis (1966-1995)
10.
SIAM
Review (1959-1995)
11.
Transactions
of the American Mathematical Society (1900-1995)
Philosophy
(10 journals)
1.
Ethics
(1938-1995)
2.
Journal
of Philosophy (1921-1995)
3.
Journal
of Symbolic Logic (1936-1996)
4.
Mind
(1876-1993)
5.
Nous
(1967-1995)
6.
Philosophical
Perspectives (1987-1995)
7.
Philosophical
Quarterly (1950-1995)
8.
Philosophical
Review (1892-1997)
9.
Philosophy
and Phenomenological Research (1940-1995)
10.
Philosophy
and Public Affairs (1971-1995)
Coauthors
of Alfred Tarski
(From: Erdos1, Version 2001, January 30, 2001
This is a list of the 507 co-authors of Paul Erdos, together with their
co-authors listed beneath them. The date of first joint paper with Erdos is
given, followed by the number of joint publications (if it is more than
one). An asterisk following the name
indicates that this Erdos co-author is known to be deceased. Please send
corrections and comments to <grossman@oakland.edu>.)
TARSKI, ALFRED*
1943: 2
Andreka, Hajnal
Banach, Stefan
Beth, Evert W.
Chang, Chen Chung
Chin, Louise H.
Doner, John E.
Erdos, Paul
Fell, James M. G.
Givant, Steven R.
Henkin, Leon A.
Horn, Alfred
Jonsson, Bjarni
Keisler, H. Jerome
Kuratowski, Kazimierz
Lindenbaum, A.
Maddux, Roger D.
McKinsey, J. C. C.
Monk, J. Donald
Mostowski, Andrzej
Nemeti, Istvan
Schwabhauser, Wolfram
Scott, Dana S.
Sierpinski, Waclaw
Smith, Edgar C., Jr.
Szczerba, Leslaw W.
Szmielew, Wanda
Vaught, Robert L.
A real quote (according to MacTutor) of Tarski:
“You will not find in semantics any remedy for decayed teeth
or illusions of grandeur or class conflict”
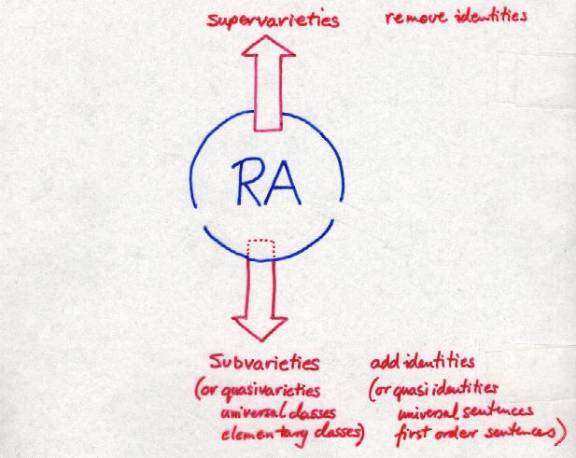
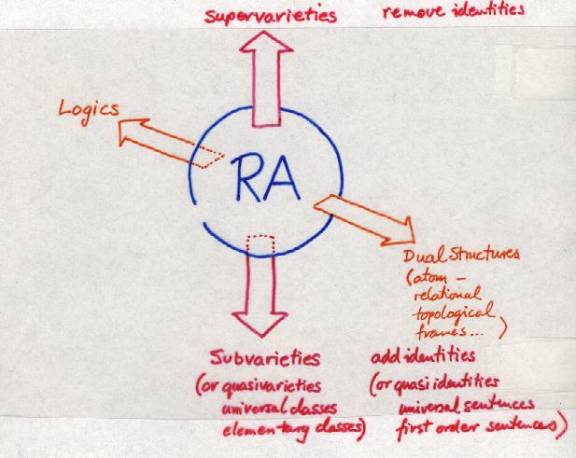
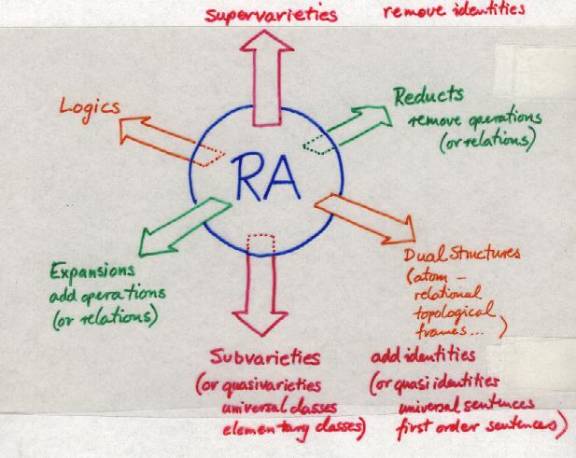
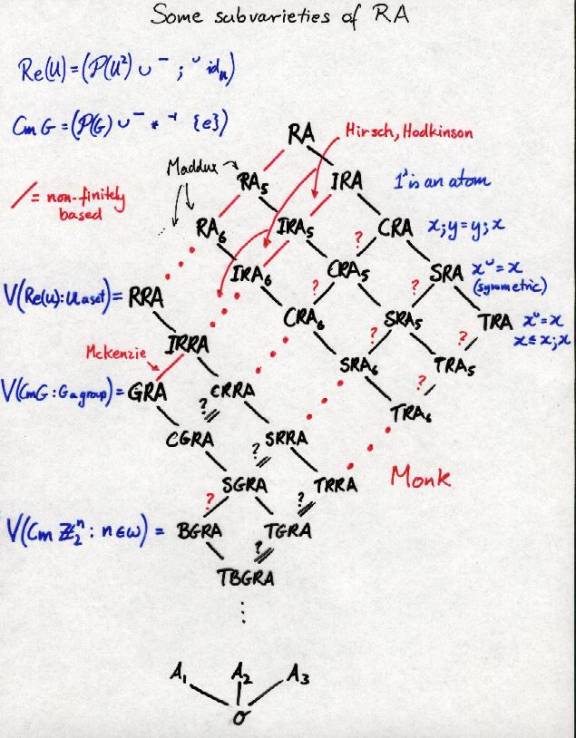
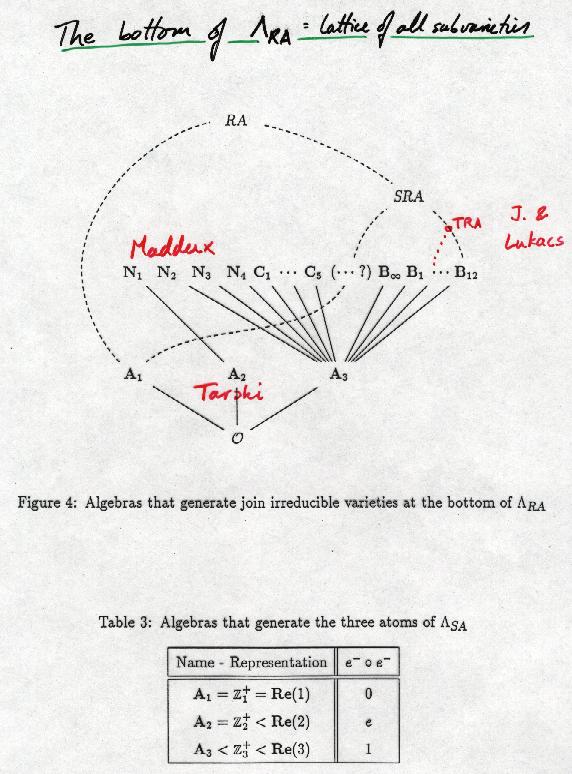
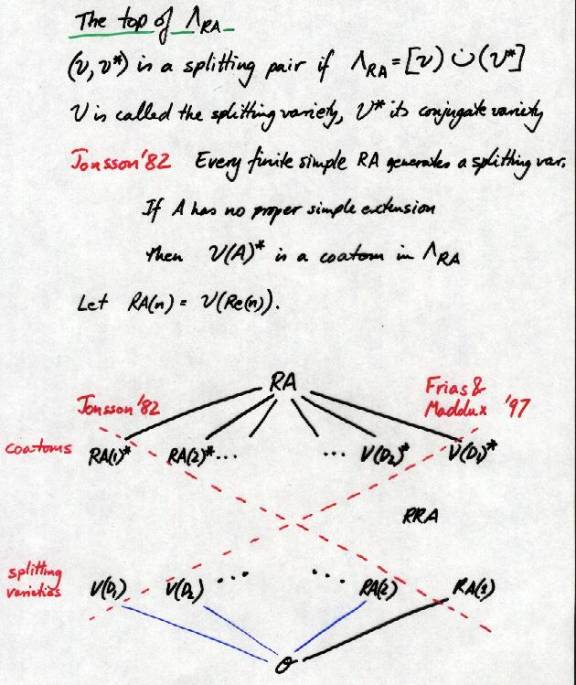
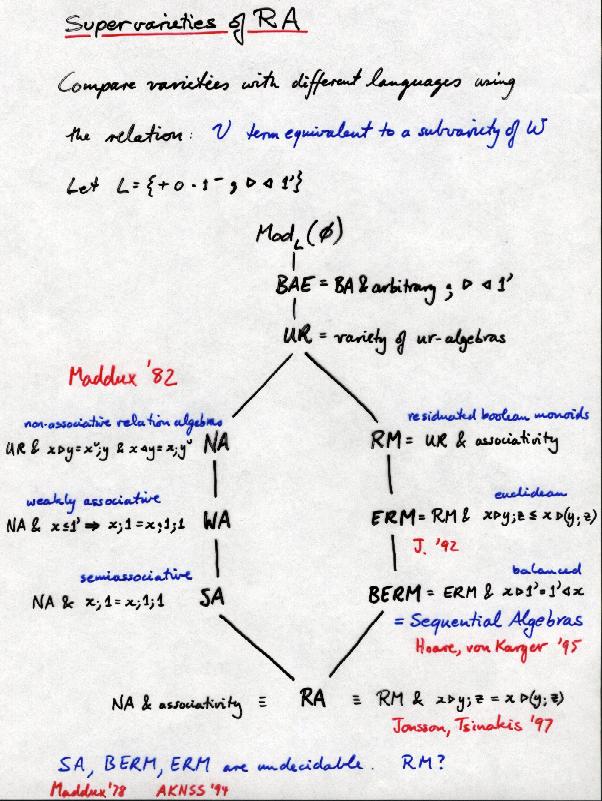
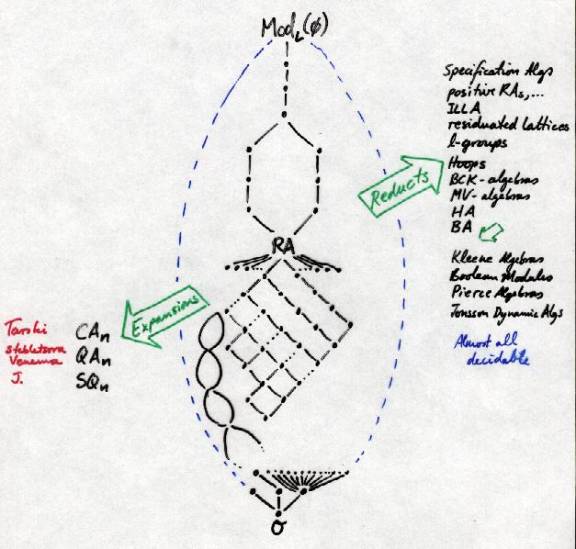
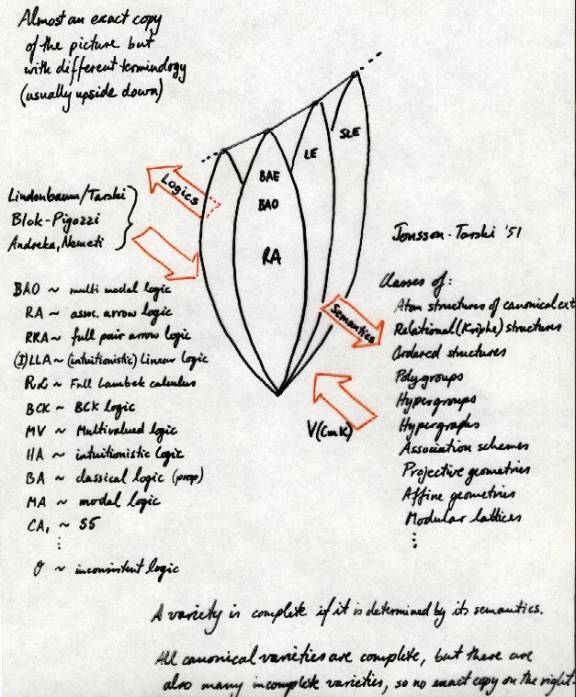
A tour of theories and structures close to relation
algebras. We start with the variety RA.
Here is the definition of Relation Algberas as recorded by Bjarni
Jonsson in a seminar that Alfred Tarski gave at Berkeley in the 1940s. Note
that the equational axiomatisation is not chosen as the original definition,
but rather it is derived from the more useful and compact quasi-equational
definition.
First some preliminaries: (A groupoid is what is nowadays
called a monoid)
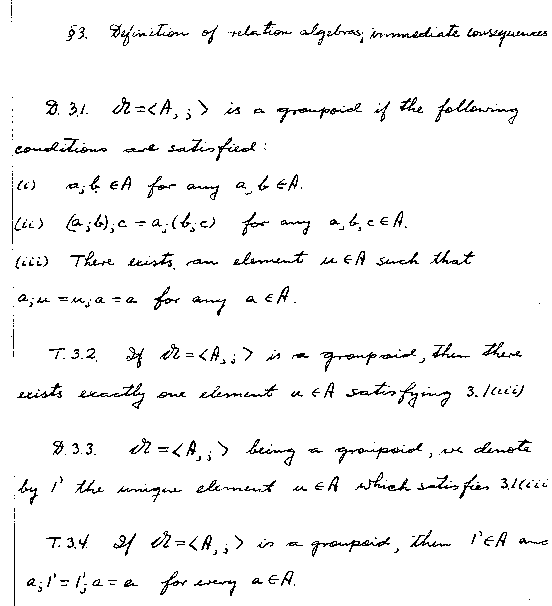
Now the definition:
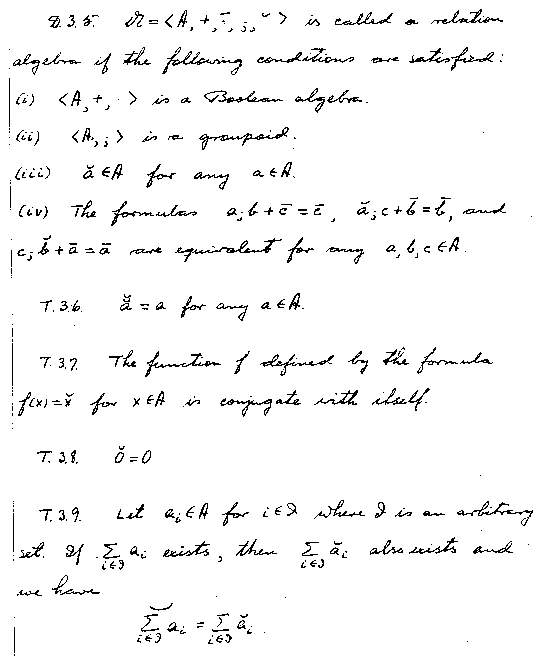
And finally the equivalent equational definition:
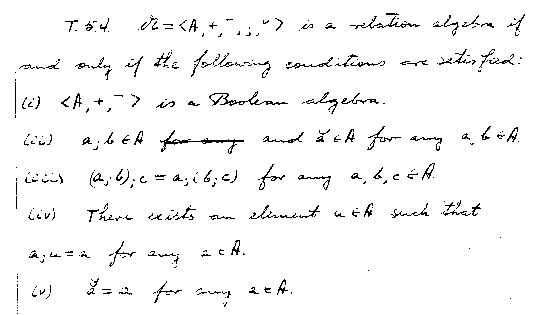
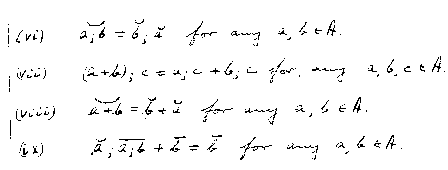
An interactive definition of Relation Algebras can be found
at http://www.math.vanderbilt.edu/~pjipsen/PCP/PCPothers.html
And now for a look at the many descendants of Relation
Algebras: